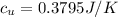Question

The Starship Enterprise is caught in a time warp and Spock is forced to use the primitive techniques of the 20th century to determine the specific heat capacity of an unknown mineral. The 128-g sample was heated to 96.2°C and placed into a calorimeter containing 77.2 g of water at 20.0°C. The heat capacity of the calorimeter was 13.9 J/K. The final temperature in the calorimeter was 23.3°C. What is the specific heat capacity (in J/g°C) of the mineral? Enter to 4 decimal places.

Answer 1

`c_u=0.3795J/K`

Step-by-step explanation:

The heat released by the unknown mineral (
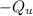`-Q_u`, where we will use the minus sign to indicate release of heat) is the heat absorbed by the calorimeter with water
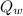`Q_w`, so we can write:

`-Q_u=Q_w`

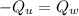
The formula that relates heat with the mass of a material, its specific heat capacity and the temperature difference it suffers because of that heat is:

`Q=mc \Delta T=mc(T_f-T_i)`

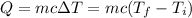
So we substitute this into the previous equation to get:

`-m_uc_u(T_(uf)-T_(ui))=m_wc_w(T_(wf)-T_(wi))`

Since at the end the final temperatures will be the same, namely

`T_(uf)=T_(wf)=T_(f)`

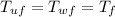
We can write

`-m_uc_u(T_f-T_(ui))=m_wc_w(T_f-T_(wi))`

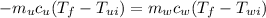
Since what we want is the specific heat capacity of the unknown mineral
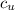`c_u`, we can write:

`c_u=-(m_wc_w(T_f-T_(wi)))/(m_u(T_f-T_(ui)))`

In this particular equation it is not necessary to transform g to Kg (since the units of masses are cancelling out) or Celsius to Kelvin (since temperature is only appearing as a difference), but if one is not sure, the units should be transformed to S.I. since Joules is in S.I.

Finally then we have:

`c_u=-((77.2g)(13.9J/K)(23.3C-20.0C))/(128g(23.3C-96.2C))=0.37949717078J/K`

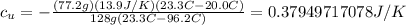
Since it asks for 4 decimal places, this must be written as:

`c_u=0.3795J/K`