Question

The relationship between the amount of money x that Cannon Precision Instruments spends on advertising and the company's total sales S(x) is given by the following function where x is measured in thousands of dollars. S(x) = −0.002x3 + 0.4x2 + 9x + 500 (0 ≤ x ≤ 200) Find the rate of change of the sales with respect to the amount of money spent on advertising.

Answer 1

S'(x)=-0.006x2+0.8x+9

Explanation:

The rate of change of the sales S(x) with respect to the amount of money spent on advertising x is then the derivative of S(x) with respect to x. What we have to calculate is S'(x).

We know that the derivative of
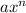`ax^n` is
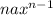`nax^(n-1)` (where a is a constant), and the derivative of a sum is the sum of the derivatives, so we can calculate the derivative of each term independently:

S'(x)=(−0.002x3 + 0.4x2 + 9x + 500)'=(−0.002)(3)x2 + (0.4)(2)x + 9

Which means:

S'(x)=-0.006x2+0.8x+9