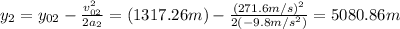Question

A toy rocket, launched from the ground, rises vertically with an acceleration of 28 m/s 2 for 9.7 s until its motor stops. Disregarding any air resistance, what maximum height above the ground will the rocket achieve? The acceleration of gravity is 9.8 m/s 2 .

Answer 1

5080.86m

Step-by-step explanation:

We will divide the problem in parts 1 and 2, and write the equation of accelerated motion with those numbers, taking the upwards direction as positive. For the first part, we have:

`y_1=y_(01)+v_(01)t+(a_1t^2)/(2)`

`v_1=v_(01)+a_1t`

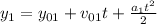
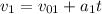
We must consider that it's launched from the ground (
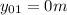`y_(01)=0m`) and from rest (
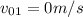`v_(01)=0m/s`), with an upwards acceleration
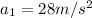`a_(1)=28m/s^2` that lasts a time t=9.7s.

We calculate then the height achieved in part 1:

`y_1=(0m)+(0m/s)t+((28m/s^2)(9.7s)^2)/(2)=1317.26m`

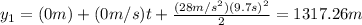
And the velocity achieved in part 1:

`v_1=(0m/s)+(28m/s^2)(9.7s)=271.6m/s`

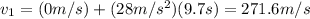
We do the same for part 2, but now we must consider that the initial height is the one achieved in part 1 (
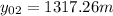`y_(02)=1317.26m`) and its initial velocity is the one achieved in part 1 (
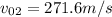`v_(02)=271.6m/s`), now in free fall, which means with a downwards acceleration
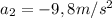`a_(2)=-9,8m/s^2`. For the data we have it's faster to use the formula
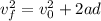`v_f^2=v_0^2+2ad`, where d will be the displacement, or difference between maximum height and starting height of part 2, and the final velocity at maximum height we know must be 0m/s, so we have:

`v_(02)^2+2a_2(y_2-y_(02))=v_2^2=0m/s`

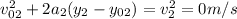
Then, to get
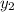`y_2`, we do:

`2a_2(y_2-y_(02))=-v_(02)^2`

`y_2-y_(02)=-(v_(02)^2)/(2a_2)`

`y_2=y_(02)-(v_(02)^2)/(2a_2)`

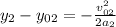
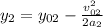
And we substitute the values:

`y_2=y_(02)-(v_(02)^2)/(2a_2)=(1317.26m)-((271.6m/s)^2)/(2(-9.8m/s^2))=5080.86m`