Question

A car is traveling at a constant negative velocity of 8.0 m/s. The driver steps on the brakes. The car slows to a stop. The car travels 20.0 m while it is slowing down. What is the magnitude of its acceleration? [HINT: You do not need to know time to solve this.]

Answer 1

Step-by-step explanation:

We need to use the formula
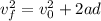`v_f^2=v_0^2+2ad` (proof at the end), where the square of the final velocity is equal to the square of the initial velocity plus to times the product of the acceleration suffered and the displacement done. We have everything except the acceleration, which we proceed to calculate as:

`v_f^2=v_0^2+2ad`

`v_f^2-v_0^2=2ad`

`a=(v_f^2-v_0^2)/(2d)`

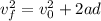
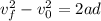
Substituting the values we have then:

`a=((0m/s)^2-(8m/s)^2)/(2(20m))=1.6m/s^2`

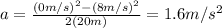
In case one wants to know where the original formula comes from, I'll derive it from the equations
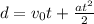`d=v_0t+(at^2)/(2)` and
`v=v_0+at`.

We obtain t from the last equation:

`t=(v-v_0)/(a)`

And substitute it on the other one:

`d=v_0t+(at^2)/(2)=v_0(v-v0)/(a)+(a)/(2)((v-v_0)/(a))^2=(v_0(v-v_0))/(a)+((v-v_0)^2)/(2a)`

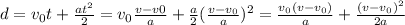
Multiplying all by 2a we get:

`2ad=2v_0(v-v_0)+(v-v_0)^2`

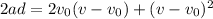
And working out the right hand side we obtain:

`2v_0(v-v_0)+(v-v_0)^2=2v_0v-2v_0^2+v^2+v_0^2-2vv_0=v^2-v_0^2`

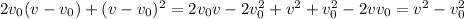
So we got
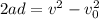`2ad=v^2-v_0^2`, which is the formula we started with.