Answer:
a) The maximun volume of air in the climber's lungs is
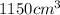
b) The climber takes 26 breaths per minute
Explanation:
a) The function is given by
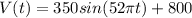 , where
, where
 is in
is in
 , and
, and
 is in minutes.
is in minutes.
So the first step is to derive it, by the chain rule we obtain
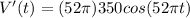 .
.
After that, we make the expression equals to zero,
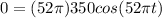 , then
, then
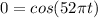 . This leads to
. This leads to
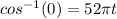 .
.
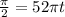 , and clearing it for
, and clearing it for
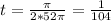 .
.
The second step is to evaluate the original expression for this value so,
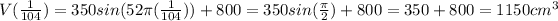 .
.
b) As we can see this function have the form
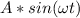 , where
, where
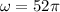 is the angular frequency, so every
is the angular frequency, so every
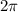 radians we will have a breath, therefore Breaths Per Minute=
radians we will have a breath, therefore Breaths Per Minute=
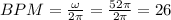 .
.