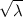Answer:
2.24
Explanation:
The probability formula using a Poisson distribution is:
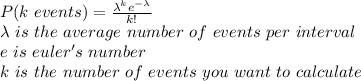
λ = 90 / 18 = 5 average goals per interval (interval = a game)
So if for example you were interested in the probability of making 2 goals in a game
k = 2
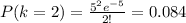
This was just an example,
The standard deviation is