Answer:
a) V = -0.227 mV
b) V = -0.5169 mV
Step-by-step explanation:
a)
Inside a sphere with a uniformly distributed charge density, electric field is radial and has a magnitude
E = (qr) / (4πε₀R³)
As we know that
V = -
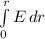
By solving above equation, we get
V = (-qr²) / (8πε₀R³)
When
R = 1.81 cm
r = 1.2 cm
q = +2.80 fC
ε₀ = 8.85 × 10⁻¹²
V = (-2.80 × 10⁻¹⁵ × (1.2 × 10⁻²)²) / (8 × 3.14 × 8.85 × 10⁻¹² × (1.81 × 10⁻²)³)
V = -2.27 × 10⁻⁴ V
V = -0.227 mV
b)
When
r = R
R = 1.81 cm
q = +2.80 fC
ε₀ = 8.85 × 10⁻¹²
V = (-qR²) / (8πε₀R³)
V = (-q) / (8πε₀R)
V = (-2.80 × 10⁻¹⁵) / (8 × 3.14 × 8.85 × 10⁻¹² × (1.81 × 10⁻²))
V = -5.169 × 10⁻⁴ V
V = -0.5169 mV