Question

A mathematics textbook has 100 pages on which typographical errors in the equations could occur. Suppose there are in fact two pages with errors. What is the probability that a random sample of 20 pages will contain at least one error?

Answer 1

0.0396

Explanation:

the probability of one page having an error is p= 2/100 = 1/50

if the letter q is the probability of not having an error then q = 49/50

Using binomial probability:

`b(x;n,p) = (n!)/(x!(n-x)!)p^xq^(n-x)`

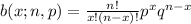
n is the sample size--> n = 20

And we want the probability that a random sample of 20 pages will contain at least one error, this is the same as 1 minus the probability of none of the 20 pages containing an error:

probability(x ≥ 1) = 1 - probability( x = 0)

Using the binomial probability equation

Probability( x=0 ) =
`b(0;20,1/50) = (20!)/(0!(20-0)!)(1/50)^0(49/50)^(2-0)`

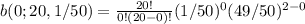
Probability( x=0 ) =
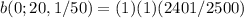`b(0;20,1/50) = (1)(1)(2401/2500)` = 0.9604

Thus,

probability(x ≥ 1) = 1 - 0.9604= 0.0396