Answer:
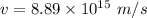
Step-by-step explanation:
An electron is released at rest from point A. It moves in response to the electric field of a fixed charge distribution along a path that takes it through point B.
Potential at point A,

Potential at point B,
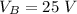
Let v is the speed of the electron as it passes point B. It can be calculated using the conservation of energy theorem as :
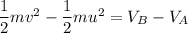
Here, u = 0
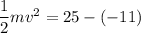
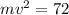

m is the mass of electron
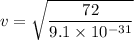
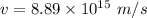
So, the electron's speed as it passes point B is
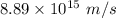 . Hence, this is the required solution.
. Hence, this is the required solution.