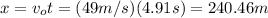Question

An Alaskan rescue plane traveling 49 m/s drops a package of emergency rations from a height of 118 m to a stranded party of explorers. The acceleration of gravity is 9.8 m/s 2 . Where does the package strike the ground relative to the point directly below where it was released?

Answer 1

240.46 m

Step-by-step explanation:

If the point in x where the package was dropped is x = 0. We can find the value of x where the package ends with the formula:

`x=v_(o)t`

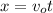
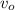`v_(o)` is the initial velocity, in this case is 49m/s

t is the time it takes for the package to get to the ground, wich we can found with the next formula:

`y = h - (1)/(2)gt^2`

where h is the height: 118 m

and
`g = 9.8m/s^2`

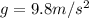
solving for t:

`t =\sqrt{(y-h)/(-(1)/(2) g) }`

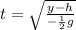
since the ground is the point where y = 0, we have:

`t=\sqrt{(2h)/(g) }`

`t=\sqrt{(2(118m))/(9.8m/s^2)} = 4.91s`

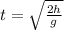
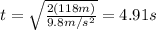
Going back to the first formula for the distance x:

`x=v_(o)t = (49m/s)(4.91s)= 240.46m`