Answer: The correct option is
(C) The rate of Hose A is 1 gallon per minute more than the rate of Hose B.
Step-by-step explanation: Given that Hose A fills a water truck at the constant rate of 60 gallons every 15 minutes.
Hose B fills a water truck at a constant rate that is represented by the function y = 3x, where y is the total number of gallons filled in x minutes.
We are to select the statement that best compares the rates of the two horses.
For Hose A :
In every 15 minutes, number of gallons filled = 60.
So, in every 1 minute, number of gallons filled is given by
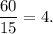
That is, Hose A is filled at the rate of 4 gallons per minute.
For Hose B :
The given function is y = 3x, where y is the total number of gallons filled in x minutes.
So, in 1 minute, number of gallons filled = 3 × 1 = 3.
That is, Hose B is filled at the rate of 3 gallons per minute.
Therefore, we get
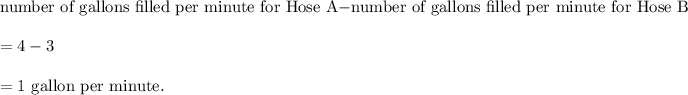
Thus, the rate of Hose A is 1 gallon per minute more than the rate of Hose B.
Option (C) is CORRECT.