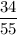Question

The board of directors of Saner Automatic Door Company consists of 12 members, 3 of whom are women. A new policy and procedures manual is to be written for the company. A committee of three is randomly selected from the board to do the writing. What is the probability that at least one member of the committee is a woman

Answer 1

Answer:
`(34)/(55)`

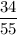
Explanation:

Given : The board of directors of Saner Automatic Door Company consists of 12 members, 3 of whom are women.

Number of Men = 12-3=9

Now, the probability that at least 1 member of the committee is a woman= 1- Probability all members are men. (1)

Number of combinations of choosing all men members =
`^9C_3`

`=(9!)/(3!(9-3)!)=84`

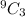
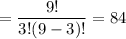
Number of combinations of choosing any 3 members out of 12

=
`^(12)C_3=(12!)/(3!(12-3)!)=220`

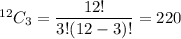
Probability that all members of the committee are men=
`(84)/(220)`

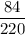
Now, from (1)

The probability that at least 1 member of the committee is a woman will be

`=1-(84)/(220)\\\\=(220-84)/(220)\\\\=(136)/(220)\\\\=(34)/(55)`

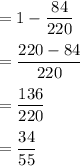
Hence, the probability that at least 1 member of the committee is a woman=
`(34)/(55)`