Question

Suppose that X is a random variable with mean 30 and standard deviation 4. Also suppose that Y is a random variable with mean 50 and standard deviation of 8. Assume that the correlation between X and Y is zero. Find the variance and the standard deviation of the random variable Z for each of the following cases. Show work.

(a) Z = 35 -10X
(b)Z = 12X - 5
(c) Z = X +Y
(d) Z = X -Y
(e) Z = -2X + 2Y

Answer 1

To find the variance and standard deviation of a random variable Z, we can use specific formulas for each case. The formulas depend on the linear combination of random variables given by Z. (a) For Z = 35 - 10X, the variance is (-10)^2 * 4 and the standard deviation is |-10| * 2. (b) For Z = 12X - 5, the variance is (12)^2 * 4 and the standard deviation is |12| * 2. (c) For Z = X + Y, the variance is 4 + 8 and the standard deviation is 2 + 2. (d) For Z = X - Y, the variance is 4 + 8 and the standard deviation is 2 + 2. (e) For Z = -2X + 2Y, the variance is (-2)^2 * 4 + 2^2 * 8 and the standard deviation is |-2| * 2 + |2| * 4.

Step-by-step explanation:

The variance and standard deviation of a linear combination of random variables can be calculated using the following formulas:

(a) For Z = 35 - 10X:

• Variance: Var(Z) = (-10)2 * Var(X) = (-10)2 * 4
• Standard Deviation: SD(Z) = |-10| * SD(X) = |-10| * 2

(b) For Z = 12X - 5:

• Variance: Var(Z) = (12)2 * Var(X) = (12)2 * 4
• Standard Deviation: SD(Z) = |12| * SD(X) = |12| * 2

(c) For Z = X + Y:

• Variance: Var(Z) = Var(X) + Var(Y) = 4 + 8 = 12
• Standard Deviation: SD(Z) = SD(X) + SD(Y) = 2 + 2 = 4

(d) For Z = X - Y:

• Variance: Var(Z) = Var(X) + Var(Y) = 4 + 8 = 12
• Standard Deviation: SD(Z) = SD(X) + SD(Y) = 2 + 2 = 4

(e) For Z = -2X + 2Y:

• Variance: Var(Z) = (-2)2 * Var(X) + 22 * Var(Y) = 4 * 4 + 16 * 8 = 64 + 128 = 192
• Standard Deviation: SD(Z) = |-2| * SD(X) + |2| * SD(Y) = 2 * 2 + 2 * 4 = 4 + 8 = 12

Answer 2

a) Var[z] = 1600

D[z] = 40

b) Var[z] = 2304

D[z] = 48

c) Var[z] = 80

D[z] = 8.94

d) Var[z] = 80

D[z] = 8.94

e) Var[z] = 320

D[z] = 17.88

Step-by-step explanation:

In general

V([x+y] = V[x] + V[y] +2Cov[xy]

how in this problem Cov[XY] = 0, then

V[x+y] = V[x] + V[y]

Also we must use this properti of the variance

V[ax+b] =
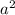`a^(2)`V[x]

and remember that

standard desviation =
`√(Var[x])`

a) z = 35-10x

Var[z] =
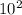`10^(2)` Var[x] = 100*16 = 1600

D[z] =
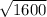`√(1600)` = 40

b) z = 12x -5

Var[z] =
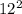`12^(2)` Var[x] = 144*16 = 2304

D[z] =
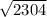`√(2304)` = 48

c) z = x + y

Var[z] = Var[x+y] = Var[x] + Var[y] = 16 + 64 = 80

D[z] =
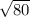`√(80)` = 8.94

d) z = x - y

Var[z] = Var[x-y] = Var[x] + Var[y] = 16 + 64 = 80

D[z] =
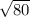`√(80)` = 8.94

e) z = -2x + 2y

Var[z] = 4Var[x] + 4Var[y] = 4*16 + 4*64 = 320

D[z] =
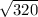`√(320)` = 17.88