Answer:
a) Var[z] = 1600
D[z] = 40
b) Var[z] = 2304
D[z] = 48
c) Var[z] = 80
D[z] = 8.94
d) Var[z] = 80
D[z] = 8.94
e) Var[z] = 320
D[z] = 17.88
Step-by-step explanation:
In general
V([x+y] = V[x] + V[y] +2Cov[xy]
how in this problem Cov[XY] = 0, then
V[x+y] = V[x] + V[y]
Also we must use this properti of the variance
V[ax+b] =
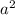 V[x]
V[x]
and remember that
standard desviation =
![√(Var[x])](https://img.qammunity.org/2020/formulas/mathematics/high-school/9trmnkfaqmn9jelsyp7lu58qlyp7zy28pr.png)
a) z = 35-10x
Var[z] =
 Var[x] = 100*16 = 1600
Var[x] = 100*16 = 1600
D[z] =
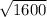 = 40
= 40
b) z = 12x -5
Var[z] =
 Var[x] = 144*16 = 2304
Var[x] = 144*16 = 2304
D[z] =
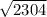 = 48
= 48
c) z = x + y
Var[z] = Var[x+y] = Var[x] + Var[y] = 16 + 64 = 80
D[z] =
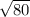 = 8.94
= 8.94
d) z = x - y
Var[z] = Var[x-y] = Var[x] + Var[y] = 16 + 64 = 80
D[z] =
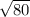 = 8.94
= 8.94
e) z = -2x + 2y
Var[z] = 4Var[x] + 4Var[y] = 4*16 + 4*64 = 320
D[z] =
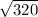 = 17.88
= 17.88