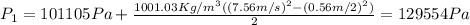Answer:
The pressure of the water in the pipe is 129554 Pa.
Step-by-step explanation:
There are wrongly written values on the proposal, the atmospheric pressure must be 101105 Pa, and the density of water 1001.03 kg/m3, those values are the ones that make sense with the known ones.
We start usign the continuity equation, and always considering point 1 a point inside the pipe and point 2 a point in the nozzle:
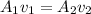
We want
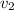 , and take into account that the areas are circular:
, and take into account that the areas are circular:
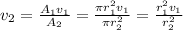
Substituting values we have (we don't need to convert the cm because they cancel out between them anyway):
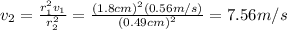
For determining the absolute pressure of the water in the pipe we use the Bernoulli equation:
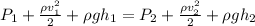
Since the tube is horizontal
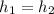 and those terms cancel out, so the pressure of the water in the pipe will be:
and those terms cancel out, so the pressure of the water in the pipe will be:
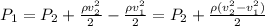
And substituting for the values we have, considering the pressure in the nozzle is the atmosphere pressure since it is exposed to it we obtain: