Question

Consult Multiple-Concept Example 15 to review the concepts on which this problem depends. Water flowing out of a horizontal pipe emerges through a nozzle. The radius of the pipe is 1.8 cm, and the radius of the nozzle is 0.49 cm. The speed of the water in the pipe is 0.56 m/s. Treat the water as an ideal fluid, and determine the absolute pressure of the water in the pipe. (The atmosphere pressure is P = 1.01 105 Pa, and the density of water is rho = 1.00 103 kg/m3.)

Answer 1

The pressure of the water in the pipe is 129554 Pa.

Step-by-step explanation:

There are wrongly written values on the proposal, the atmospheric pressure must be 101105 Pa, and the density of water 1001.03 kg/m3, those values are the ones that make sense with the known ones.

We start usign the continuity equation, and always considering point 1 a point inside the pipe and point 2 a point in the nozzle:

`A_1v_1=A_2v_2`

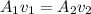
We want
`v_2`, and take into account that the areas are circular:

`v_2=(A_1v_1)/(A_2)=(\pi r_1^2 v_1)/(\pi r_2^2)=(r_1^2 v_1)/(r_2^2)`

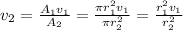
Substituting values we have (we don't need to convert the cm because they cancel out between them anyway):

`v_2=(r_1^2 v_1)/(r_2^2)=((1.8cm)^2 (0.56m/s))/((0.49cm)^2)=7.56m/s`

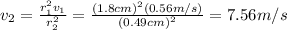
For determining the absolute pressure of the water in the pipe we use the Bernoulli equation:

`P_1+(\rho v_1^2)/(2)+\rho gh_1=P_2+(\rho v_2^2)/(2)+\rho gh_2`

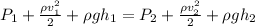
Since the tube is horizontal
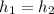`h_1=h_2` and those terms cancel out, so the pressure of the water in the pipe will be:

`P_1=P_2+(\rho v_2^2)/(2)-(\rho v_1^2)/(2)=P_2+(\rho (v_2^2-v_1^2))/(2)`

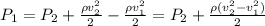
And substituting for the values we have, considering the pressure in the nozzle is the atmosphere pressure since it is exposed to it we obtain:

`P_1=101105 Pa+(1001.03Kg/m^3 ((7.56m/s)^2-(0.56m/2)^2))/(2)=129554 Pa`