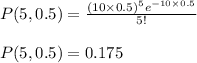Answer with Step-by-step explanation:
We know from Poisson distribution
The probability that a random process with an average arrival rate of λ occurs 'n' times in time interval of 't' is given by
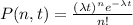
Part a)
The probability for 5 calls in 1 hour is
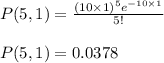
Part b)
Probability of 3 or fewer calls occurs in 1 hour is the sum of the following probabilities
1) Only 1 call occurs in 1 hour.
2) Only 2 calls occurs in 1 hour.
3) Only 3 calls occurs in 1 hour.
4) There is no cal in 1 hour.
Thus we can write
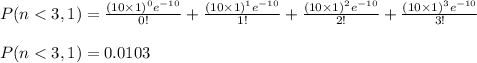
Part c)
The probability for 15 calls in 2 hours is

Part d)
The probability for 5 calls in 30 minutes or 0.5 hours is