Answer:
a) What is the energy of the n = 5 level?
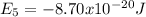
(b) Calculate the wavelength and frequency of a photon emitted when an electron jumps down from n = 5 to n = 1 in a H atom.
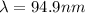 ,
,
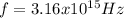
Step-by-step explanation:
The permitted energy for the atom of hydrogen according with the Bohr's model is defined as:
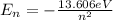 (1)
(1)
Or it can be expressed in Joules, since

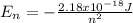
Where the value
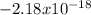 represents the energy of the ground state¹ and n is the principal quantum number.
represents the energy of the ground state¹ and n is the principal quantum number.
a) What is the energy of the n = 5 level?
For the case of
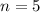 :
:
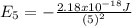
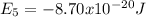
So the energy of the
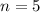 level is
level is
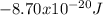 .
.
(b) Calculate the wavelength and frequency of a photon emitted when an electron jumps down from n = 5 to n = 1 in a H atom.
The wavelength can be determined by means of the Rydberg formula:
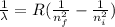 (2)
(2)
Where R is the Rydberg constant, with a value of
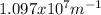
For this particular case
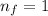 and
and
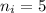 :
:
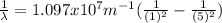
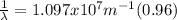
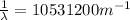
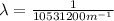
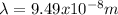
Where
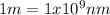
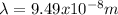 .
.

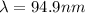
The frequency can be found by means of:
 (3)
(3)
Equation (3) can be rewritten in terms of
 :
:
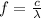
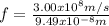
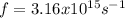
Where
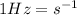
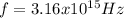
Key terms:
¹Ground state: State of minimum energy.