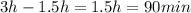Question

Tom and Linda stand at point A. Linda begins to walk in a straight line away from Tom at a constant rate of 2 miles per hour. One hour later, Tom begins to jog in a straight line in the exact opposite direction at a constant rate of 6 miles per hour. If both Tom and Linda travel indefinitely, what is the positive difference, in minutes, between the amount of time it takes Tom to cover the exact distance that Linda has covered and the amount of time it takes Tom to cover twice the distance that Linda has covered?

A. 60B. 72C. 84D. 90E. 108

Answer 1

The difference is D. 90 min

Explanation:

The distance that Linda covers (DL) in terms of time in hours (t) is:

`DL=2mph*t`

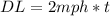
and the distance that Tom covers (DT) in terms of time in hours (t) is:

`DT=6mph*(t-1)`

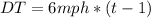
We need to subtract 1 hour from Tom's time because he started walking an hour later than Linda.

When Tom has covered the same distance that Linda has, DT=DL, so:

`2mph*t=6mph(t-1)`

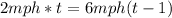
solving for t, we will find the time Tom needs to cover the same distance as Linda:

`2t=6t-6`

`2t-6t=-6`

`t=(6)/(4)=1.5h`

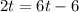
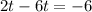
Now, when Tom has covered twice the distance than Linda, DT=2DL, so:

`6mph(t-1)=2*2mph*t`

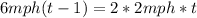
Again, solving for t:

`6t-6=4t`

`6t-4t=6`

`t=(6)/(2)=3h`

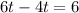
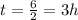
So, the difference between those two times is:

`3h-1.5h=1.5h=90min`