Question

1) Target sells 24 bottles of water for $3 and 36 bottles of water for $4. Which is the better buy and by how much?

A) 24 bottles for $3 by 1.5¢ per bottle
B) 24 bottles for $3 by 70¢ per bottle
C) 24 bottles for $3 by 75¢ per bottle
D) 36 bottles for $4 by 1.4¢ per bottle

2) An ice machine uses 3 gallons of water every 9 hours. How many gallons of water does it use each hour? How many hours does it take to use one gallon? A) 1/9 gallons per hour; 1 hour
B) 1/3 gallons per hour; 3 hours
C) 3 gallons per hour; 1/9 hour
D) 1/3 gallons per hour; 1/3 hour

3) If a dozen eggs cost $1.35, what is the unit cost?
A) $0.11
B) $0.13
C) $1.23
D) $4.29

4) Suppose Anna earns $38.50 to walk the neighbor's dog 7 hours during the week. How much does Anna earn per hour?
A) $4.25
B) $4.80
C) $5.50
D) $5.75

5) Which ratio is equivalent to the unit rate of "30 miles 1 gallon"? How was the unit rate transformed into the equivalent ratio?
A) "3 gallons 10 miles;" by dividing the numerator and denominator of the unit rate by 10.
B) "90 miles 5 gallons;" by multiplying the numerator and denominator of the unit rate by 3.
C) "6 gallons 180 miles;" by multiplying the numerator and denominator of the unit rate by 2.
D) "180 miles 6 gallons;" by multiplying the numerator and denominator of the unit rate by 6.

Answer 1

Part 1) option D) 36 bottles for $4 by 1.4¢ per bottle

Part 2) option B) 1/3 gallons per hour; 3 hours

Part 3) option A) $0.11

Part 4) option C) $5.50

Part 5) option D) "180 miles 6 gallons;" by multiplying the numerator and denominator of the unit rate by 6.

Explanation:

Part 1) we know that

To find out the unit rate divide the total cost by the number of bottles

a) sells 24 bottles of water for $3

The unit rate is

`(3)/(24)= \$0.125\ per\ bottle`

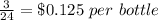
b) sells 36 bottles of water for $4

The unit rate is

`(4)/(36)= \$0.111\ per\ bottle`

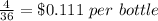
The better buy is 36 bottles of water for $4 (because the unit rate is less)

Find out the difference

`\$0.125-\$0.111=\$0.014`

`\$0.014=1.4c`

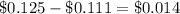
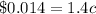
therefore

36 bottles for $4 by 1.4¢ per bottle

Part 2) we know that

An ice machine uses 3 gallons of water every 9 hours

a) How many gallons of water does it use each hour?

using proportion

Let

x ----> the number of gallons

`(3)/(9)(gal)/(h)=(x)/(1)(gal)/(h)\\\\x=3/9\\\\x=1/3\ gal`

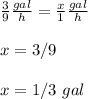
b) How many hours does it take to use one gallon?

using proportion

Let

x ----> the number of hours

`(3)/(9)(gal)/(h)=(1)/(x)(gal)/(h)\\\\x=9/3\\\\x=3\ h`

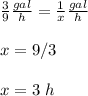
therefore

1/3 gallons per hour; 3 hours

Part 3) we know that

To find out the unit cost divide the total cost by the number of eggs

`(1.35)/(12)=\$0.11\ per\ egg`

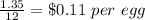
Part 4) we know that

To find out how much Anna earn per hour divide the total earned by the number of hours

`(38.50)/(7)=\$5.50\ per\ hour`

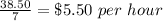
Part 5) Which ratio is equivalent to the unit rate of "30 miles 1 gallon"? How was the unit rate transformed into the equivalent ratio?

we have the ratio

`(30)/(1)(miles)/(gallon)=30(miles)/(gallon)`

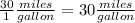
Verify each case

a) "3 gallons 10 miles;"

we have

`(10)/(3)(miles)/(gallon)=3.33(miles)/(gallon)`

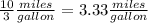
This ratio is not equivalent to the given ratio

b) "90 miles 5 gallons;"

we have

`(90)/(5)(miles)/(gallon)=18(miles)/(gallon)`

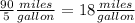
This ratio is not equivalent to the given ratio

c) "6 gallons 180 miles;"

we have

`(180)/(6)(miles)/(gallon)=30(miles)/(gallon)`

This ratio is equivalent to the given ratio by by multiplying the numerator and denominator of the unit rate by 6.

d) "180 miles 6 gallons;"

we have

`(180)/(6)(miles)/(gallon)=30(miles)/(gallon)`

This ratio is equivalent to the given ratio by by multiplying the numerator and denominator of the unit rate by 6.

therefore

"180 miles 6 gallons;" by multiplying the numerator and denominator of the unit rate by 6.