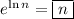Not sure why my previous answer was deleted...
If you substitute
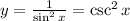 , then
, then
 gives
gives
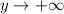 , so the limit is equal in value to
, so the limit is equal in value to
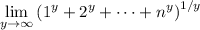
Since
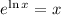 , we can write
, we can write
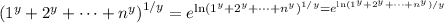
Because
 is continuous at all
is continuous at all
 , we can pass the limit to the argument of the exponential function. That is,
, we can pass the limit to the argument of the exponential function. That is,
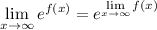
so that the limit we're interested in is equal to
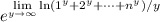
For all natural numbers
 , we have
, we have
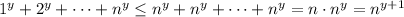
so
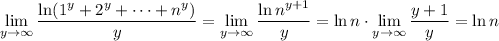
and this makes the overall limit take on a value of