Question

Consider a two-period model of a perfectly competitive firm that owns the rights to a finite deposit of a non-renewable resource. The firm’s total recoverable reserve of the resource is 575 tons, which the firm expects to extract fully over two periods. The firm’s total extraction costs are given by the function ????(qt)=0.1qt2. The market price of the resource is expected to remain constant at $110 per ton. The market interest rate is 10 percent.(a) Solve for the firm’s efficient extraction quantities in each of the two periods.(b) Confirm that the efficient extraction quantities are consistent with the Hotelling rule.

Answer 1

first year = 300

second year = 275

Step-by-step explanation:

The cost will be for year 1 and year 2 extractions for the first year we must consider the cost is increased by the rate as it could be used to invest at 10%

`tq=0.1Q_1^(2)(1+0.1) + 0.1Q_2\: ^(2)`

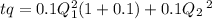
we revenue will be the first year plus the interest.

And then, second year revenue

`TR = 110Q_1 (1+0.1) + 110Q_2`

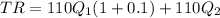
Profit will be revenue less cost:

`Profit = TR - TC\\110Q_1 (1+0.1) + 110Q_2 - 0.1Q_1^(2)(1.1) - 0.1Q_2\: ^(2)`

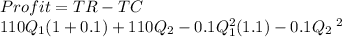
lastly, we know the total amount we an extras is 575 tons so

q1 + q2 = 575

We can replace Q2 as an expression of q1

q2 = 575 - q1

and now we try to solve to get the quadratic.

`Profit = 110Q_1 (1+0.1) + 110(575-Q1) - 0.1Q_1^(2)(1.1) - 0.1(575-Q1)\: ^(2)`

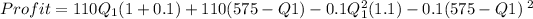
121Q1 + 63250 - 110Q1 -0.11Q2 - 33,062.5‬ +115q1 -0.1Q12

126Q1 + 30,187.5 - 0.21Q12

-0.21Q2 + 126Q + 30,187.5

As this is a quadratic function the max point will be at vertex

now we solve for the vertex of the quadratic function

-b/2a

126/0.21*2 = -104/0.4 = 300

Q1 max out the profit at 300

Q2 will be 575 - 300 = 275