Answer:
first year = 300
second year = 275
Step-by-step explanation:
The cost will be for year 1 and year 2 extractions for the first year we must consider the cost is increased by the rate as it could be used to invest at 10%
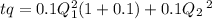
we revenue will be the first year plus the interest.
And then, second year revenue
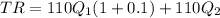
Profit will be revenue less cost:
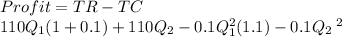
lastly, we know the total amount we an extras is 575 tons so
q1 + q2 = 575
We can replace Q2 as an expression of q1
q2 = 575 - q1
and now we try to solve to get the quadratic.
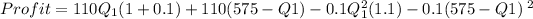
121Q1 + 63250 - 110Q1 -0.11Q2 - 33,062.5 +115q1 -0.1Q12
126Q1 + 30,187.5 - 0.21Q12
-0.21Q2 + 126Q + 30,187.5
As this is a quadratic function the max point will be at vertex
now we solve for the vertex of the quadratic function
-b/2a
126/0.21*2 = -104/0.4 = 300
Q1 max out the profit at 300
Q2 will be 575 - 300 = 275