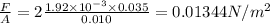Question

A very large plate is placed equidistant between two vertical walls. The 10-mm spacing between the plate and each wall is filled with a liquid of absolute viscosity 1.92 x 10^-3 Pa.s. Determine the force per unit plate area required to move the plate upward at a speed of 35 mm/s. Assume linear variation of velocity between the plate and the walls.

Answer 1

Force per unit plate area is 0.1344
`N/m^(2)`

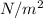
Solution:

As per the question:

The spacing between each wall and the plate, d = 10 mm = 0.01 m

Absolute viscosity of the liquid,
`\mu =1.92* 10^(- 3) Pa-s`

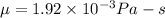
Speed, v = 35 mm/s = 0.035 m/s

Now,

Suppose the drag force that exist between each wall and plate is F and F' respectively:

Net Drag Force = F' + F''

`F = \tau A`

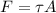
where

`\tau` = shear stress

A = Cross - sectional Area

Therefore,

Net Drag Force, F =
`(\tau ' +\tau '')A`

`(F)/(A) = \tau ' +\tau ''`

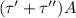
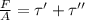
Also

F =
`(\mu v)/(d)`

where

`\mu` = dynamic coefficient of viscosity

Pressure, P =
`(F)/(A)`

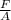
Therefore,

`(F)/(A) = (\mu v)/(d) + (\mu v)/(d) = 2(\mu v)/(d)`

`(F)/(A) = 2(1.92* 10^(- 3)* 0.035)/(0.010) = 0.01344 N/m^(2)`