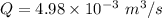Answer:
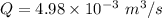
Step-by-step explanation:
Given that
L= 50 m
Pressure drop = 130 KPa
For Copper tube is 3/4 standard type K drawn tube
Outside diameter=22.22 mm
Inside diameter=18.92 mm
Dynamic viscosity for kerosene
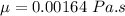
Pressure difference given as
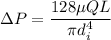
Where
L is length of tube
μ is dynamic viscosity
Q is volume flow rate
d is inner diameter of tube
ΔP is pressure drop
Now by putting the values
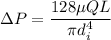
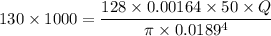
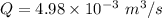
So flow rate is