Answer:
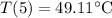
Well, In my opinion, it's still warm enough to drink
Step-by-step explanation:
Let's use Newton's Law of Cooling given by:
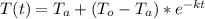 (1)
(1)
Where:
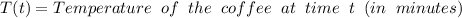
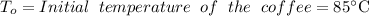
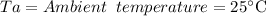
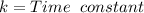
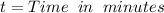
Replacing the data provide in (1)
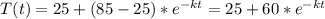 (2)
(2)
So, we need to find k. But we know:
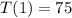
Using that information in (2)
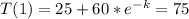 (3)
(3)
Solving for k in (3)
Sustract 25 to both sides:
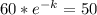
Multiply both sides by
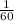
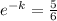
Express
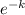 as
as
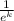
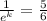
Natural logarithm to both sides:
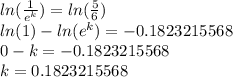
Replacing k in (2)
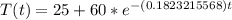 (4)
(4)
Evaluating t=5 in (4)
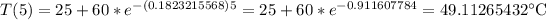
I attached you the graph of the function (4)