Question

Write the expression for work performed by expansion/compression. Define all terms in this expression. Give the SI and English units for each term. an ideal gas during isothermal

Answer 1

`W=P_1V_1\ ln(V_2)/(V_1)`

Step-by-step explanation:

Lets take

At initial position

`Pressure = P_1`

`Volume = V_1`

At final position

`Pressure = P_2`

`Volume = V_2`

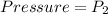
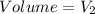
SI unit

`Pressure =N/m^2`

`Volume =m^3`

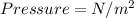
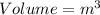
English units

`Pressure =lb/in^2`

`Volume =in^3`

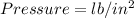
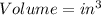
For expansion process:

As we know that work done given as

`W=\int P.dV`

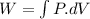
We know that for isothermal process

P.V = C

`P_1V_1=P_2V_2=C`

`W=\int_(V_1)^(V_2)(P_1V_1)/(V).dV`

`W=P_1V_1\ ln(V_2)/(V_1)`

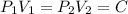
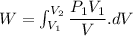
Expression for expansion and for compression will be same.