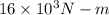Answer:
Tension in wire will be
Step-by-step explanation:
We have given seed of the transverse wave v = 400 m/sec
Linear density = 0.10 g/cm
We know that 1 gram = 0.001 kg
And 1 cm = 0.01 m
So
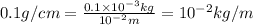
We know that speed of wave is given by
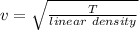 , here T is tension in the wire
, here T is tension in the wire
So
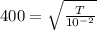
Squaring both side
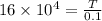
T =
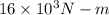
So tension in wire will be