Question

PLEASE HELP!!

Consider the functions f(x)=3x+30 and g(x)=x^2+20. At what positive integer value of x does the quadratic function, g(x) begin to exceed the linear function f(x)?

Answer 1

x=5

Explanation:

We are given that

`f(x)=3x+30`

`g(x)=x^2+20`

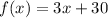
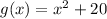
We have to find the positive integer value of x for which the quadratic function g(x) begin to exceed the linear function f(x).

`g(x) > f(x)`

`x^2+20 > 3x+30`

`x^2+20-3x-30 >0`

`x^2-3x-10 > 0`

`(x-5)(x+2) > 0`

`x-5 > 0`

`x > 5`

`x+2 > 0`

`x >-2`

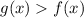
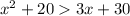
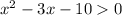
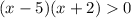
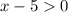
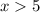
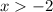
Interval (
`5,\infty)`

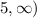
Therefore , g(x) exceed f(x) in the interval (
`5,\infty)`.

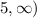g(x) begin to exceed the linear function at x=5

Answer 2

`x\in(-\infty,-2)\cup(5,\infty)`

Explanation:

The duadratic function
`g(x)=x^2+20` begin to exceed the linear function
`f(x)=3x+30` when
`g(x)>f(x)`

Solve this inequality:

`x^2+20>3x+30\\ \\x^2-3x+20-30>0\\ \\x^2-3x-10>0\\ \\x^2-5x+2x-10>0\\ \\x(x-5)+2(x-5)>0\\ \\(x-5)(x+2)>0`

This inequality is equivalent to

`\left[\begin{array}{l}\left\{\begin{array}{l}x-5>0\\x+2>0\end{array}\right.\\ \\\left\{\begin{array}{l}x-5<0\\x+2<0\end{array}\right.\end{array}\right.\Rightarrow \left[\begin{array}{l}\left\{\begin{array}{l}x>5\\x>-2\end{array}\right.\\ \\\left\{\begin{array}{l}x<5\\x<-2\end{array}\right.\end{array}\right.\Rightarrow \left[\begin{array}{l}x>5\\ \\x<-2\end{array}\right.`

Answer:
`x\in(-\infty,-2)\cup(5,\infty)`