Question

PLEASE HELP ASAP!!!

Using the graph of f(x) and g(x), where g(x) = f(k⋅x), determine the value of k.

A. 4
B. 1/4
C. -1/4
D. -4

Answer 1

Based on the graph, at x=1 g(x)=10 and at x=4 f(x)=10. If g(x)=f(k•x), x is being multiplied by k in areas with the same value. x=1 and so to reach 4 it has to be multiplied by 4. Therefore k=4

Answer 2

Answer: The correct option is

(A) 4.

Step-by-step explanation: We are given the graphs of f(x) and g(x) where

g(x) = f(k⋅x).

We are to determine the value of k.

From the graph, we note that

(1, 10) is a point on g(x) and (4, 10) is a point on f(x).

That is, at y = 10, f(x) = g(x).

Therefore, we get

`f(4)=g(1)\\\\\Rightarrow f(4)=f(k* 1)\\\\\Rightarrow k=4.`

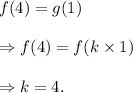
Thus, the required value of k is 4.

Option (A) is CORRECT.