Question

What, roughly, is the percent uncertainty in the volume of a spherical beach ball whose radius is 5.66 0.09 m?

Answer 1

• 4.77 %

Step-by-step explanation:

We know that the volume V for a sphere of radius r is

`V(r) = (4)/(3) \ \pi \ r^3`

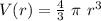
If we got an uncertainty
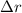`\Delta r` the formula for the uncertainty of V is:

`\Delta V(r) = \sqrt{  ((dV)/(dr) \Delta r)^2  }`

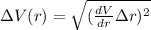
We can calculate this uncertainty, first we obtain the derivative:

`(dV)/(dr)  = 3 * (4)/(3) \ \pi \ r^2`

`(dV)/(dr)  = 4 \ \pi \ r^2`

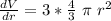
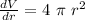
And using it in the formula:

`\Delta V(r) = √(  (4 \ \pi \ r^2\Delta r)^2  )`

`\Delta V(r) = √(  4^2 \ \pi^2 \ r^4 \Delta r^2  )`

`\Delta V(r) =  4 \  \pi \ r^2 \Delta r`

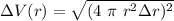
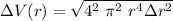
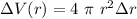
The relative uncertainty is:

`(\Delta V(r))/(V(r))`

`( 4 \  \pi \ r^2 \Delta r  )/( (4)/(3) \ \pi \ r^3)`

`( 3  \Delta r  )/(  r)`

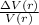
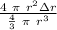
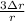
Using the values for the problem:

`( 3 * 0.09 m  )/(  5.66 m) = 0.0477`

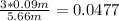
This is, a percent uncertainty of 4.77 %