Question

A speedy rabbit is hopping to the right with a velocity of 4.0m/s when it sees a carrot in the distance. The rabbit speeds up to its maximum velocity of 13m/s with a constant acceleration 2.0m/s2 rightward.

How many seconds does it take the rabbit to speed up from 4.0m/s to 13m/s

Answer 1

t = 4.5 seconds

Explanation:

initial velocity = 4.0 m/s

final velocity = 13 m/s

acceleration = 2.0 m/s2

t = (final velocity - initial velocity) / acceleration

t = (13 - 4.0) / 2.0

t = 4.5 seconds

Answer 2

4.5 sec.

Explanation:

We know that:

`v_(0)=4.0m/s`

`v_(f)=13m/s`

`a=2.0m/s^(2)`

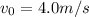
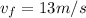
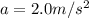
Now, to calculate the time, we must use this equation:

`v_(f)=v_(0)+at\\v_(f)-v_(0)=at\\(v_(f)-v_(0))/(a)=t \\t=(13m/s-4m/s)/(2m/s^(2) ) =4.5sec`

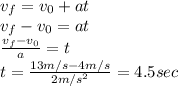
This means that the rabbit needs 4.5 seconds to speed up from 4m/s to 13 m/s. In this type of problem, we just need to read carefully if there are initial (
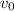`v_(0)`) and final speed (
`v_(f)`), and acceleration, because that's the case when we use the equation showed.