Question

A theater has a seating capacity of 750 and charges $3 for children, s5 for students, and $7 for adults. At a certain screening with fll ttendance, there were combined. The receipts totaled $3450. How many children attended the show?

Answer 1

Between 150 and 450

Explanation:

We are going to find the number by resolving a system of linear equations.

First we write the system equations :

`C+S+A=750`

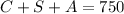
Where C : children, S : students and A : adults

The equation represents the ''full attendance''

The second equation :

`3C+5S+7A=3450`

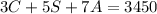
This equation represents the totaled receipts.

The system :

`C+S+A=750\\3C+5S+7A=3450`

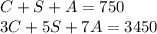
has the following associated matrix :

`\left[\begin{array}{cccc}1&1&1&750\\3&5&7&3450\end{array}\right]`

By performing elementary matrix operations we find that the matrix is equivalent to

`\left[\begin{array}{cccc}1&0&-1&150\\0&1&2&600\\\end{array}\right]`

The new system :

`C-A=150\\S+2A=600`

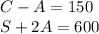
Working with the equations :

`C = 150 + A\\S = 600-2A`

Our solution vector is :

`\left[\begin{array}{c}C&S&A\end{array}\right] =\left[\begin{array}{c}150+A&600-2A&A\end{array}\right]`

For example :

If 0 adults attended ⇒ A = 0

`C = 150 + 0 \\C = 150\\S = 600 - 2A\\S = 600`

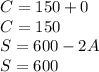
This verify the totaled receipts equation :

150($3)+600($5) = $ 3450

A ≥ 0 ⇒ If A = 0 ⇒ C = 150

C = 150 is the minimum children attendance

From the equation :

`S = 600 -2A`

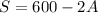
S ≥0

600 - 2A ≥ 0

600 ≥ 2A

300≥ A

A is restricted to the interval [ 0, 300]

When A = 0 ⇒ C = 150

When A = 300 ⇒C = 150 + A = 150 + 300 = 450

Children ∈ [ 150,450]

With C being an integer number (including 0)

Also S and A are integer numbers (including 0)