Answer:
Between 150 and 450
Explanation:
We are going to find the number by resolving a system of linear equations.
First we write the system equations :
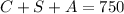
Where C : children, S : students and A : adults
The equation represents the ''full attendance''
The second equation :
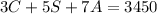
This equation represents the totaled receipts.
The system :
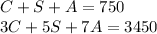
has the following associated matrix :
![\left[\begin{array}{cccc}1&1&1&750\\3&5&7&3450\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/d42lwmqxtnqh4l81t0llk54g6zx91oqn7k.png)
By performing elementary matrix operations we find that the matrix is equivalent to
![\left[\begin{array}{cccc}1&0&-1&150\\0&1&2&600\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/ovgw8u0s9h5o4151hiofjczlk7pdo7cefk.png)
The new system :
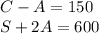
Working with the equations :
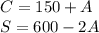
Our solution vector is :
![\left[\begin{array}{c}C&S&A\end{array}\right] =\left[\begin{array}{c}150+A&600-2A&A\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/f4v6ov5rqne8b3hqowztomcww3v6iso16x.png)
For example :
If 0 adults attended ⇒ A = 0
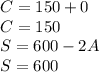
This verify the totaled receipts equation :
150($3)+600($5) = $ 3450
A ≥ 0 ⇒ If A = 0 ⇒ C = 150
C = 150 is the minimum children attendance
From the equation :
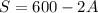
S ≥0
600 - 2A ≥ 0
600 ≥ 2A
300≥ A
A is restricted to the interval [ 0, 300]
When A = 0 ⇒ C = 150
When A = 300 ⇒C = 150 + A = 150 + 300 = 450
Children ∈ [ 150,450]
With C being an integer number (including 0)
Also S and A are integer numbers (including 0)