Question

A student measured the lead content of a paint sample 4 times. The standard deviation of the measurements was found to be 1.5% of the average. Calculate the confidence interval at the 90% confidence level. confidence interval: Can this student be 90% confident that the true value is within 1.8% of the measured average? O yes O no

Answer 1

Yes. There is 90% confidence the mean will be between ± 1.76% of the sample average.

Explanation:

In this case, where the sample is little and the standard deviation of the population is unknown, the confidence interval (CI) can be expressed as

`\bar{x}\pm t_(n-1)*s/√(n)`

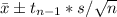
"s" is the standard deviation of the sample and t(n-1) is the critical t-value with (n-1) degrees of freedom. In this case, the degrees of freedom ar (4-1)=3.

The standard deviation is expressed as 1.5% or the mean, that is

`s=0.015*\bar{x}`

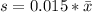
Since we have two limits for the mean and a 90% CI, we have 5% of being outside the confidence. Looking up in the table for P(x>t)=0.05 and DF=3, we have

`t_3=2.353`

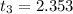
Then the CI is

`\bar{x} \pm 2.353*(0.015*\bar{x})/√(4)\\\\\bar{x} \pm 2.353*(0.015*\bar{x})/√(4)\\\\\bar{x} \pm 0.0176\bar{x}`

There is 90% confidence the mean will be between ± 1.76% of the sample average.