Question

Match each differential equation to a function which is a solution.

FUNCTIONS
A. y=3x+x2y=3x+x2,
B. y=e−4xy=e−4x,
C. y=sin(x)y=sin⁡(x),
D. y=x12y=x12,
E. y=6e3xy=6e3x,

Differential Equations

1. y″+y=0y″+y=0
2. y′=3yy′=3y
3. 2x2y″+3xy′=y2x2y″+3xy′=y
4. y″+6y′+8y=0y″+6y′+8y=0

Answer 1

Answer: 1 - C

2 - E

3 - no answer

4 - B

Explanation:

A.
`y = 3x+x^2`

`y' = 3 + 2x\\y'' = 2`

• Replace in 1:

`y'' + y = 0`

`2 + 3x + x^2 \\eq 0`

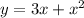
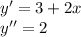
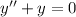
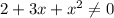
So, A is not an answer for 1

• Replace in 2:

`y' = 3y`

`3+2x = 3(3x + x^2)`

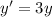
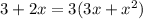
So, A is not an answer for 2

• Replace in 3

`2x^2y'' + 3xy'= y`

`2x^2(2) + 3x(3 + 2x) = 4x^2 + 9x + 6x^2 \\eq 3x+x^2`

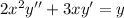
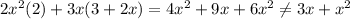
So, A is not an answer for 3

• Replace in 4

`y'' + 6y' + 8y = 0`

`2 + 6(3+2x)+8(3x + x^2) = 2+18+12x+24x+8x^2 \\eq 0`

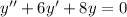
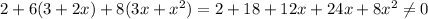
So, A is not an answer for 4

B.
`y = e^(-4x)`

`y' = -4e^(-4x)`

`y'' = 16e^(-4x)`

• Replace in 1

`y'' + y = 0`

`16e^(-4x) -4e^(-4x) = 12e^(-4x) \\eq 0`

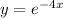
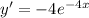
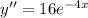
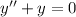
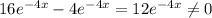
So, B is not an answer for 1

• Replace in 2

`y' = 3y`

`-4e^(-4x) \\eq 3e^(-4x)`

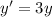
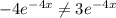
So, B is not an answer for 2

• Replace in 3

`2x^2y'' + 3xy' = y`

`2x^2(16e^(-4x)) +3x(-4e^(-4x)) \\eq  e^(-4x)`

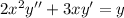
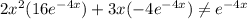
So, B is not an answer for 3

• Replace in 4

`y'' + 6y' +8y = 0`

`16e^(-4x) + 6(-4e^(-4x)) + 8e^(-4x) = e^(-4x)(16-24+8) = 0`

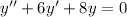
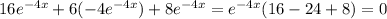
So, B is an answer for 4

C.
`y = sin(x)`

`y' = cos(x)`

`y'' = -sin(x)`

• Replace in 1

`y'' + y = 0`

`-sin(x) + sin(x) = 0`

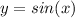
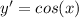
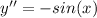
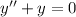
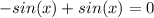
So, C is an answer for 1

We jump to

D.
`y = x^(12)`

`y' = 12x^(11)`

`y'' = 132 x^(10)`

• Replace in 2

`y' = 3y`

`12x^(11) \\eq 3x^(12)`

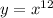
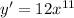
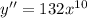
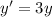
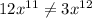
So, D is not an answer for 2

• Replace in 3

`2x^2y'' + 3xy' = y`

`2x^2(132x^(10)) + 3x(12x^(11)) = 300x^(12) \\eq x^(12)`

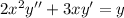
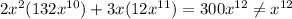
So, D is not an answer for 3

E.
`y = 6e^(3x)`

`y' = 18e^(3x)`

`y'' = 54e^(3x)`

• Replace in 2

`y' = 3y`

`18e^(3x) = 3(6e^(3x)) = 18e^(3x)`

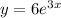
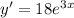
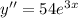
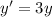
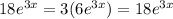
So, E is an answer for 2