Answer:
a) $121.00
b) $121.55
Explanation:
We use the formula of Future Value
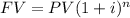
a) Future value of a deposit of $100 with an interest rate of 10% compounded annually
PV=100
i=10%
n= 2 years
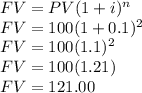
b) Future value of a deposit of $100 with an interest rate of 10% compounded semiannually
PV=100
i=10%/2=5% (When compounding semiannually, the rate is divided by the number of semesters in a year, in this case 2)
n= 4 semesters
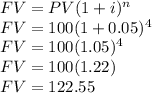
Basically, the difference is the number of periods n, in a) n=2: (1+i)^2 and in b) n=4: (1+i/2)^4.
The more n, the more the future value.