Question

Find and compare the future value after two years of a attracting interest at a rate of 10% compounded a) annually and b) semi annually. deposit of $100

Answer 1

a) $121.00

b) $121.55

Explanation:

We use the formula of Future Value

`FV= PV(1+i)^n`

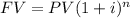
a) Future value of a deposit of $100 with an interest rate of 10% compounded annually

PV=100

i=10%

n= 2 years

`FV= PV(1+i)^n\\FV= 100(1+0.1)^(2)\\FV= 100(1.1)^(2)\\FV= 100(1.21)\\FV=121.00`

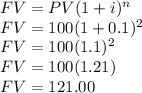
b) Future value of a deposit of $100 with an interest rate of 10% compounded semiannually

PV=100

i=10%/2=5% (When compounding semiannually, the rate is divided by the number of semesters in a year, in this case 2)

n= 4 semesters

`FV= PV(1+i)^n\\FV= 100(1+0.05)^(4)\\FV= 100(1.05)^(4)\\FV= 100(1.22)\\FV=122.55`

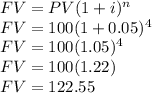
Basically, the difference is the number of periods n, in a) n=2: (1+i)^2 and in b) n=4: (1+i/2)^4.

The more n, the more the future value.