Question

at what temperature will a fixed amount of gas with a volume of 175 L at 15 degrees celsius and 760mmHg occupy a volume of 198L at a pressure of 640mmHg?

Answer 1

Answer: The temperature when the volume and pressure has changed is 274 K

Step-by-step explanation:

To calculate the pressure when temperature and volume has changed, we use the equation given by combined gas law. The equation follows:

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)`

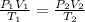
where,

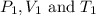`P_1,V_1\text{ and }T_1` are the initial pressure, volume and temperature of the gas

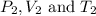`P_2,V_2\text{ and }T_2` are the final pressure, volume and temperature of the gas

We are given:

`P_1=760mmHg\\V_1=175L\\T_1=15^oC=[15+273]K=288K\\P_2=640mmHg\\V_2=198L\\T_2=?K`

Putting values in above equation, we get:

`(760mmHg* 175L)/(288K)=(640mmHg* 198L)/(T_2)\\\\T_2=274K`

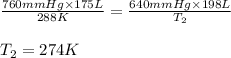
Hence, the temperature when the volume and pressure has changed is 274 K

Answer 2

T₂ = 274.5 K = 1.35 °C

Step-by-step explanation:

Given: V₁ = 175 L, P₁ = 760 mmHg, T₁ = 15°C = 288.15 K (∵ 1°C=273.15 K)

V₂ = 198 L, P₂ = 640 mmHg, T₂ = ? K

To calculate T₂, we use the General Gas Equation:
`(P_(1)V_(1))/(T_(1))= (P_(2)V_(2))/(T_(2))`

`((760 mmHg)* (175 L))/(288.15 K)= ((640 mmHg)*(198 L))/(T_(2))`

`T_(2)= (288.15 K * 640 mmHg * 198 L)/(760 mmHg* 175 L)`

`T_(2)= (36514368)/(133000) = 274.5 K`

Therefore, T₂ = 274.5 K = 1.35 °C