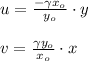Answer with Explanation:
Given that
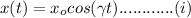
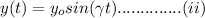
Thus by definition x component of velocity in Lagrangian system is given by
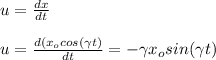
Thus by definition y component of velocity in Lagrangian system is given by
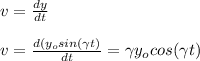
Since in eulerian system we need to eliminate time from the equations
From euations 'i' and 'ii' we can write
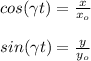
Applying these values in the velocity components as obtained in Lagrangian system we get