Answer:
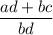
Explanation:
Let
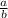 and
and
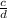 be two rational numbers, where b and d are not zero and a, b, c and d are integers.
be two rational numbers, where b and d are not zero and a, b, c and d are integers.
1. Given:
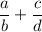
2. Multiply to get a common denominator :
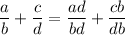
3. Simplify:
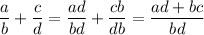
4. Since
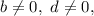 then
then
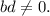
If
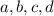 are integers, then
are integers, then
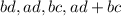 are integers too. So the fraction
are integers too. So the fraction
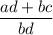
is a rational number