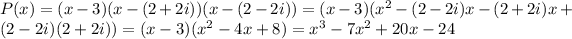Answer:
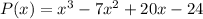
Explanation:
You are given three numbers: 3, 2+2i and 2-2i. Number 3 is a real number and numbers 2+2i and 2-2i are two conjugate complex numbers.
If the polynomial has a complex number as its root, then it also has the conjugate complex number as its root.
In your case, complex numbers 2+2i and 2-2i are conjugate to each other, so the polynomial of the smallest degree is