Question

Explain why the function of f(x)=4x^2+8x is neither even or odd

Answer 1

By putting x = -x in f(x) i.e. f(-x) we didn't get f(x) or -f(x) so, the function is neither even nor odd.

Explanation:

We need to explain why the function of
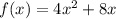`f(x)=4x^2+8x` is neither even or odd

First we will understand, when the function is even and odd

Even function:

A function is even if f(-x) = f(x)

Odd function:

A function is odd if f(-x) = -f(x)

So, if we get the above result by putting x = -x, then we can say that the function is even or odd.

If we don't get any of the above results then the function is neither even nor odd.

So, for the given function:
`f(x)=4x^2+8x`

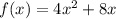
Put x = -x

`f(x)=4x^2+8x\\Put x=-x\\f(-x)=4(-x)^2+8(-x)\\f(-x)=4x^2-8x`

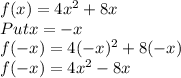
So, by putting x=-x in f(x) i.e. f(-x) we didn't get f(x) or -f(x) so, the function is neither even nor odd.