Answer:
By putting x = -x in f(x) i.e. f(-x) we didn't get f(x) or -f(x) so, the function is neither even nor odd.
Explanation:
We need to explain why the function of
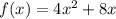 is neither even or odd
is neither even or odd
First we will understand, when the function is even and odd
Even function:
A function is even if f(-x) = f(x)
Odd function:
A function is odd if f(-x) = -f(x)
So, if we get the above result by putting x = -x, then we can say that the function is even or odd.
If we don't get any of the above results then the function is neither even nor odd.
So, for the given function:
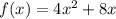
Put x = -x
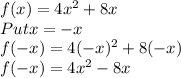
So, by putting x=-x in f(x) i.e. f(-x) we didn't get f(x) or -f(x) so, the function is neither even nor odd.