Question

The walnut Cove Ruritan Club sells hot dogs and drinks from a concession stand at the annual 4th of July parade. Carl bought 5 hot dogs and 3 drinks and paid $13.50. Susan purchased 2 hot dogs and 3 drinks and was charged $9.00. What is the cost of 1 hot dog and what is the cost of 1 drink?

Answer 1

The cost of one hot dog is $1.5 and the cost of one drink is $2.

Explanation:

Let

h = the cost of a hog dog and d = the cost of a drink

We know from the information given that:

• Carl bought 5 hot dogs and 3 drinks and paid $13.50. This is equal to
  `5\cdot h +3\cdot d=13.50`

• Susan purchased 2 hot dogs and 3 drinks and was charged $9.00. This is equal to
  `2\cdot h +3\cdot d=9.00`

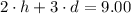
So we have a system of equations

`5\cdot h +3\cdot d=13.50\\2\cdot h +3\cdot d=9.00`

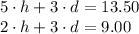
We can solve by elimination as follows:

`\mathrm{Multiply\:}5h+3d=13.5\mathrm{\:by\:}2:\\10h+6d=27\\`

`\mathrm{Multiply\:}2h+3d=9\mathrm{\:by\:}5:\\10h+15d=45`

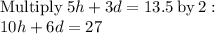
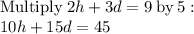
Subtract
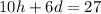`10h+6d=27` from
`10h+15d=45`

`(10h+15d=45) -(10h+6d=27)=\\9d=18`

`\mathrm{Solve}\:9d=18\:\mathrm{for}\:d:\\d=2`

`\mathrm{For\:}10h+6d=27\mathrm{\:plug\:in\:}\quad \:d=2`

`\mathrm{Solve}\:10h+6\cdot \:2=27\:\mathrm{for}\:h:\\h=(3)/(2) = 1.5`

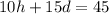
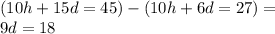
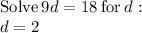
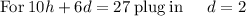
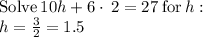
Therefore

h = $1.5 and d = $2