Answer:
From the options given, there is no correct answer in the option.
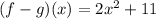
Given:
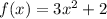
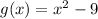
Step-by-step explanation:
From question, we need to find the subtraction of the given functions. In this step, we need to find the subtraction of the two functions. The given are functions of ‘x’.
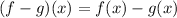
Now, we need to substitute the each functions,
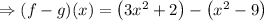
Now, we need to multiply the signs with the numbers inside the bracket,
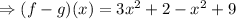
Now, on adding and subtracting,
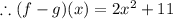
Thus, we found the subtraction of the given functions.