Question

Gabriel went to the grocery store and bought bottles of soda and bottles of juice. Each bottle of soda has 35 grams of sugar and each bottle of juice has 10 grams of sugar. Gabriel purchased 2 more bottles of soda than bottles of juice and they all collectively contain 385 grams of sugar. Determine the number of bottles of soda purchased and the number of bottles of juice purchased.

Answer 1

Gabriel bought 9 bottles of soda, and 7 bottles of sugar.

Explanation:

This problem is solved by using a system of equations.

`x` will be a bottle of soda, and
`y` will be a bottle of juice.

So, we know that each bottle of soda has 35 grams of sugar, this would expressed like:
`35x`.

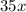In addition, each bottle of juice has 10 grams of sugar, this would be:
`10y`.

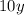Now, the problem states that the total amount of sugar is 385 grams, this allows us to represent this with the equation:

`35x+10y=385`

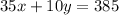
The problem specifies that Gabriel purchased 2 more bottles of soda than juice, this is represents with this equation:

`x=y+2`

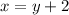
Now, we solve the system of equations 2x2, which will give us the result of each variable:

`\left \{ {{35x+10y=385} \atop {x=y+2}} \right.\\\left \{ {{35x+10y=385} \atop {(x-y=2})10} \right.\\\left \{ {{35x+10y=385} \atop (10x-10y=20}} \right.\\45x=405\\x=(405)/(45)=9`

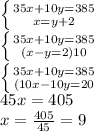
This means that Gabriel purchased 9 bottles of soda.

Then, we replace this value in one of the equation to find the other result:

`x=y+2`

`9=y+2`

`y=9-2`

`y=7`

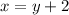
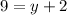
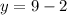
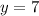
So, now we know that Gabriel bought 9 bottles of soda, and 7 bottles of sugar.

Answer 2

9 bottles of soda and 7 bottles of juice

Explanation:

Let x be the number of bottles of soda purchased and y be the number of bottles of juice purchased.

1. Gabriel purchased 2 more bottles of soda than bottles of juice, then

`x=y+2`

2. Each bottle of soda has 35 grams of sugar, then there are 35x g of sugar in x bottles of soda.

Each bottle of juice has 10 grams of sugar, then there are 10y g of sugar in y bottles of juice.

In total, there are 35x+10y g of sugar.

All bottles collectively contain 385 grams of sugar, thus

`35x+10y=385`

3. Solve the system of two equations:

`\left\{\begin{array}{l}x=y+2\\ \\35x+10y=385\end{array}\right.`

Substitute the first equation into the second equation:

`35(y+2)+10y=385\\ \\35y+70+10y=385\\ \\35y+10y=385-70\\ \\45y=315\\ \\y=7\\ \\x=7+2=9`