Answer:
the fund will be valued after 36 quarters: 443.027,75
Step-by-step explanation:
This will be an arithmetic progression with h = 500
the continously rate we are going to convert to a quarterly equivalent rate:
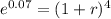
![\sqrt[4]{e^(0.07)}-1 = r__(quarter)](https://img.qammunity.org/2020/formulas/business/college/l5a1ci4kulf7tq34a8nybd69p741s50dlf.png)
r = 0.017654022
Then we calculate future value of an ordinary annuity of 1,100
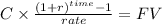
C 1,100
time 36
rate 0.017654022
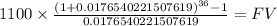
FV $54,682.8156
plus future value of the increases:
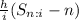
500/0.017654022 = 28,322.15773
Sn:i
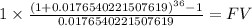
FV 49.7117
n = 36
Sn:i - n = 13.7117
$28,322.15773 x 13.7117 = $388.344,93
Now we add both:
$54,682.8156 + $388.344,93 = 443.027,75