Question

. The time spent by students working on a project is a normal random variable with parameters μ= 12 and ???? = 4. a. what is the probability that the amount of the time spent on a project is less than 14 hours? b. what is the probability that the amount of the time spent on a project is greater than 8 hours?

Answer 1

a) The probability is 0.19146.

b) The probability is 0.15866.

Explanation:

a) In this problem we have a random variable X with normal distribution, and its parameters are μ = 12 and σ = 4. The variable X stands for the amount of time that the students spend in a project. With this, our problem is to find the probability that X is less than 14. So,

`P(X\leq 14)`.

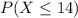Recall that the tables we have are made to calculate probabilities with standardized normal variables, this means that its mean is 0 and its standard deviation is 1. This can be done considering the variable
`Z=(x-\mu)/(\sigma). So,</p><p>[tex]P(X\leq 14) = P\left((Z-12)/(4)\leq (14-12)/(4)\right) = P(Z\leq 0.5)`.

Now, we look down the rows to find 0.5 and then across the columns to 0.00 which yield a probability of 0.19146.

b) In this case we want to calculate
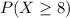`P(X\geq 8)`. We follow an analogue reasoning:

`P(X\geq 8) = P\left (Z-12)/(4)\geq (8-12)/(4)\right) = P(Z\geq -1)`

Now we use that
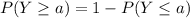`P(Y\geq a)=1-P(Y\leq a)` where Y is a random variable. Then,

`P(X\geq 8) =P(Z\geq -1) = 1 -P(Z\leq -1)`.

But,

`P(Z\leq -1) = P(Z\geq 1) = 1-P(Z\leq 1)`.

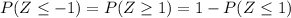Now we substitute this last value and get

`P(X\geq 8) =P(Z\geq -1) = 1 -P(Z\leq -1) = 1 - (1-P(Z\leq 1)) = P(Z\leq 1)`.

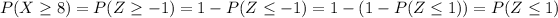Again, we look into the table and found that

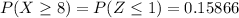`P(X\geq 8) =P(Z\leq 1) = 0.15866`.