Answer:
We reject the null hypothesis at the significance level of 0.05.
Explanation:
 vs
vs
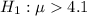 (upper-tail alternative)
(upper-tail alternative)
We have
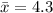 ,
,
 and n = 120. We have a large sample and our test statistic is
and n = 120. We have a large sample and our test statistic is
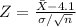 which is normal standard approximately. We have observed
which is normal standard approximately. We have observed
 .
.
We should use the significance level
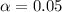 . The 95th quantile of the standard normal distribution is
. The 95th quantile of the standard normal distribution is
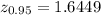 and the rejection region is given by {z > 1.6449}. Because the observed value 2.7386 is greater than 1.6449, we reject the null hypothesis at the significance level of 0.05.
and the rejection region is given by {z > 1.6449}. Because the observed value 2.7386 is greater than 1.6449, we reject the null hypothesis at the significance level of 0.05.